fit 2002 > Programmmiersprachentypen > konzeptionelle Entwicklungen und Auswirkungen > deklarative Sprachen

Überblick


Durch die deklarative Programmierweise, kann man mit Prolog quasi zweckfrei Programmieren. Dies macht Prolog z.B. für den Schulunterricht interessant, worauf im folgenden kurz eingegangen wird >[programmierstile].

Folgende Erfahrungen konnten gesammelt werden:
  • viele interessante Vorschläge, PROLOG in den Anfangsunterricht einzubeziehen
  • kein Motivationsproblem: Schüler können sehr früh mächtige Programme schreiben
  • hohes Maß an Orthogonalität


Es ergaben sich aber auch einige Mängel: Alle Vorschläge setzen voraus,

  • daß PROLOG eine große Nähe zur natürlichen Sprache besitzt,
  • daß Anfänger leichter Probleme beschreiben als Vorschriften zu ihrer Lösung angeben können, im Widerspruch zu empirischen Ergebnissen aus der Psychologie.


Prolog war von Begin an zur Verarbeitung natürlicher Sprache ausgelegt, die Popularität im Bereich der künstlichen Intelligenz kam erst später hinzu. Daraus ergibt sich eine Nähe zur natürlichen Sprache: Alltagslogik=Prädikatenlogik.

  1. Problem: Umsetzung umgangssprachlicher Aussagen mit temporalen, kausalen oder undifferenzierten logischen Operationen in prädikaten-logische Aussagen: Sie war reich, und er heiratete sie <=> Er heiratete sie, und sie war reich. Paula ist eine gute Schülerin, weil sie hart arbeitet. Wenn es regnet, nehme ich einen Schirm => Wenn es nicht regnet, nehme ich keinen Schirm.
  2. Problem: closed world assumption versus open world-Alltag: Gibt es auf Tahiti Vulkane? Mensch: weiß nicht. PROLOG: nein.
  3. Problem: Deklarative <=> prozedurale Semantik. Anfänger benötigen Verständnis für virtuelle PROLOG-Maschine

Mit Prolog kann man den Ansatz des Problemlösen durch Problembeschreiben verfolgen (basierend auf der Idee des zweckfreien Wissens, aus dem ein Computer zu einem Problem eine Lösung generiert). Tatsächlich sieht es allerdings meistens anders aus, da das eingegebene Wissen oft in hohem Maße zweckorientiert ist.

Beispiele dafür:

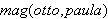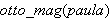Modellierungsentscheidungen: $mag(otto,paula)$ oder $otto\_mag(paula)$ oderMATH


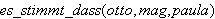
A, B und C stehen vor Gericht. A sagt aus, daß B lügt. B sagt aus, daß C lügt. C sagt aus, daß A und B lügen beide. Wer lügt, wer sagt die Wahrheit? Die PROLOG-Modellierung:
ist_Lügner(wahr,lügt).

ist_Lügner(lügt,wahr).

beide_lügen(wahr,lügt,lügt).

beide_lügen(lügt,wahr,lügt).

beide_lügen(lügt,lügt,wahr).

beide_lügen(lügt,wahr,wahr).

?- ist_Lügner(A,B),ist_Lügner(B,C),beide_lügen(C,A,B).

Beachte: Keinerlei logische Schlüsse!

Die Konsequenzen daraus sind:

  • Schüler sind nicht gut in Logik => Einführung in Prädikatenlogik nötig
  • Schüler können Modellierungprobleme nicht intuitiv lösen => Vertieftes Verständnis von PROLOG und der virtuellen PROLOG-Maschine nötig
  • Vorteile von PROLOG im Anfangsunterricht sehr zweifelhaft


Weiterführende Informationen


>[reflection] Reflection in logic, functional and object-oriented programming (paper)

>Entstehungskontext | Konzepte und Techniken | Entwicklung und Auswirkungen | Praxis | Bewertung